1. 研究背景、动机、主要贡献
DDPM的论文有指出与其他基于似然的模型相比,我们的模型不具有竞争性的对数似然。
而本文主要做的两件事情就是提高对数似然和提高采样速度。
本文还发现,DDPM 可以与 GAN 的样本质量相匹配,同时根据召回率衡量,可以实现更好的模式覆盖率。
本文还研究了 DDPM 如何随着可用训练计算量的变化而扩展,并发现更多的训练计算会带来更好的样本质量和对数似然。
2. 论文提出的新思路或新方法
2.1 提高对数似然
2.1.1 Learning
(将方差参数化为
在DDPM中,相对于方差,更多关注的是分布的均值。且利用均值相等作为条件,来推导出噪音的权重。
本文从 DDPM 中方差的设置入手(
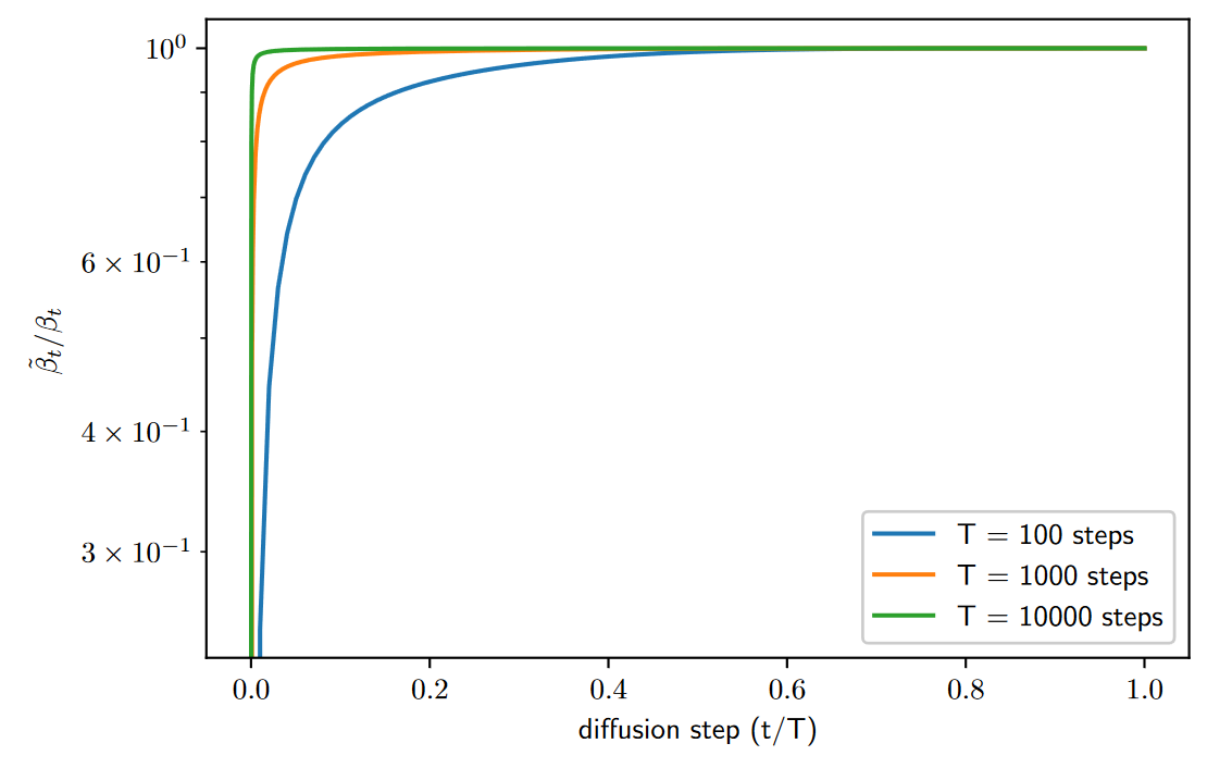
固定方差似乎是一个合理的选择,但它没有提到对数似然。事实上,显示扩散过程的前几个步骤对变分下界的贡献最大。因此,可以通过使用更好的
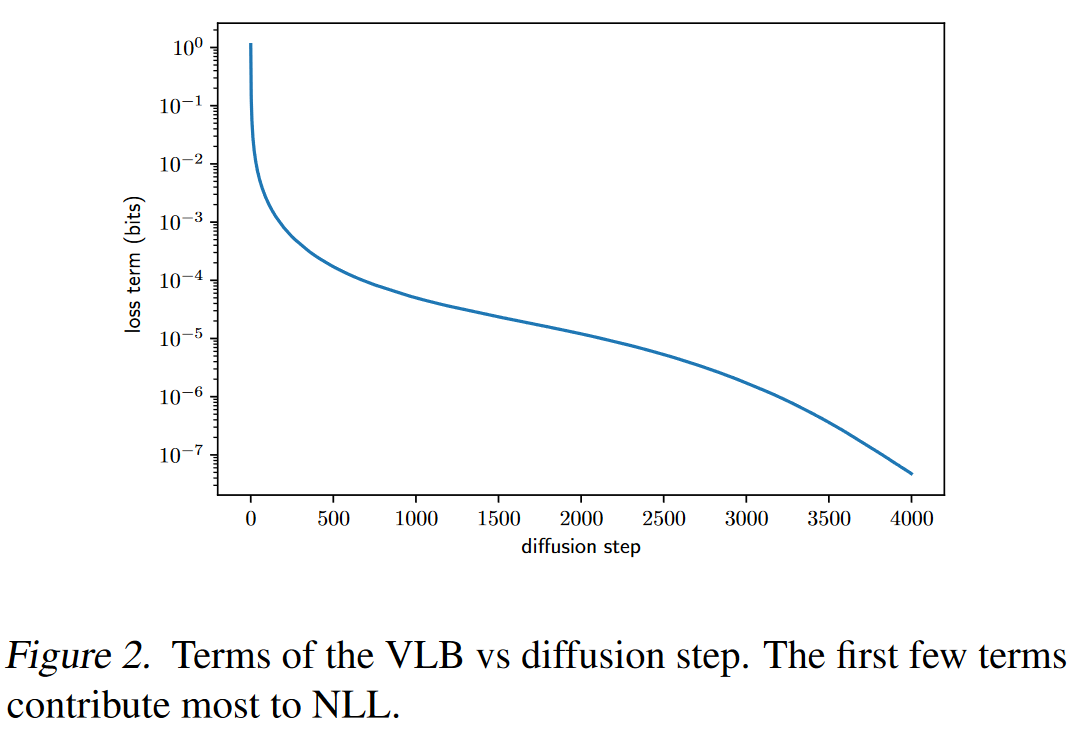
本文是将方差参数化为
2.1.2 Improving the Noise Schedule
(重新构建噪声表,使
Ho 等人使用的线性噪声表对于高分辨率图像效果很好,但对于分辨率 64 × 64 和 32 × 32 的图像来说效果不佳。
线性计划最后四分之一的潜伏几乎纯粹是噪声,而余弦计划增加噪声的速度更慢

当跳过高达20%的反向扩散过程时,用线性时间表训练的模型不会变得更糟(通过FID测量)。(就存在较多的无效时间)
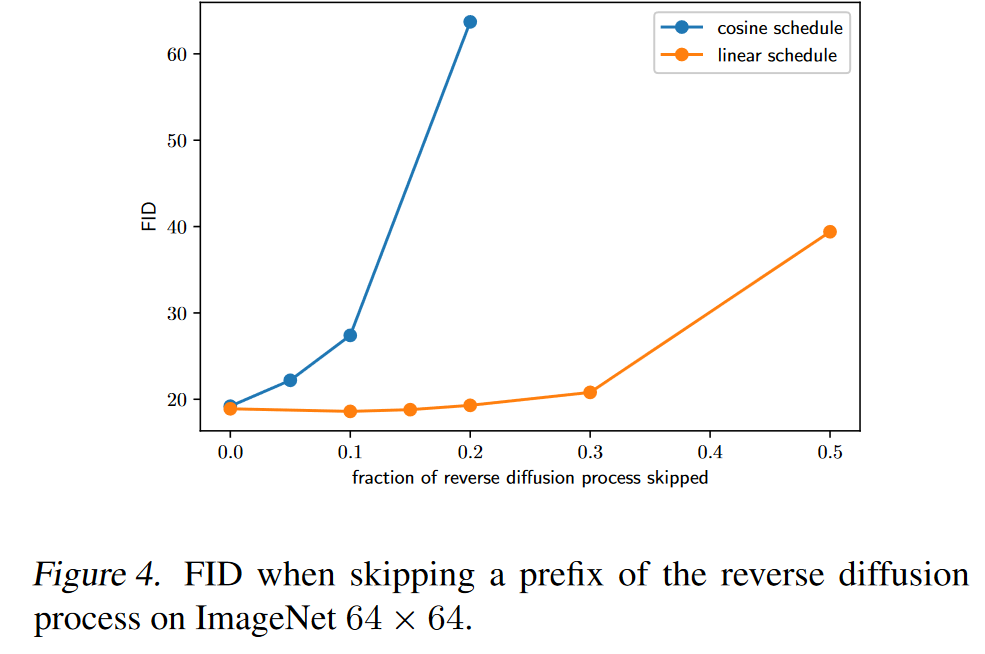
因此,重新构建噪声表
- 将
限制为不大于 0.999,以防止在扩散过程结束时接近 t = T 时出现奇点。 - 余弦时间表设计为在过程中间有一个
的线性下降,同时在 t = 0 和 t = T 的极值附近变化很小,以防止噪声水平突然变化。 - 使用较小的偏移量 s 来防止
在 t = 0 附近太小,因为在过程开始时存在少量噪声会使网络难以足够准确地进行预测。选择 s= 0.008 使得 略小于像素箱大小 1/127.5。 - 选择使用
,因为它是一个常见的数学函数,具有我们正在寻找的形状。
图 5 可以看到 Ho 等人的线性时间表下降到零的速度要快得多,信息破坏的速度比必要的要快。
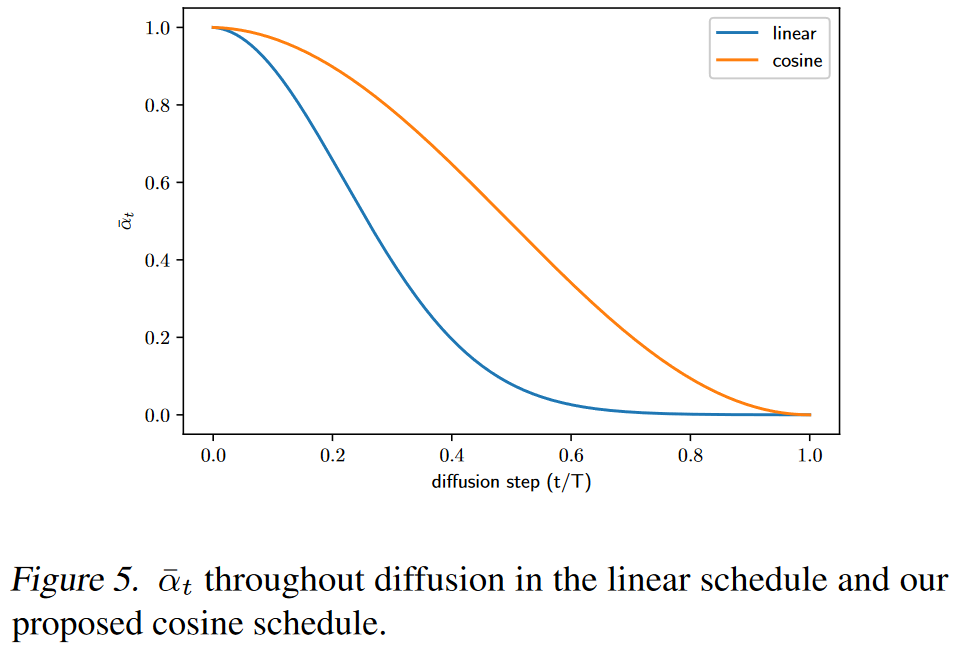
2.1.3 Reducing Gradient Noise
(重要性采样)
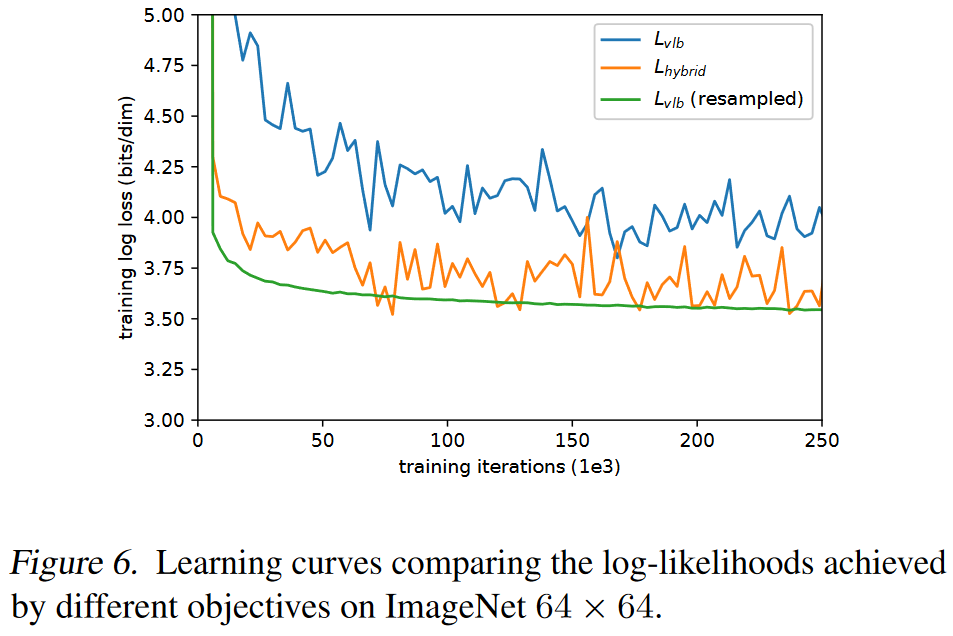

注意到
由于
2.2 Improving Sampling Speed
所有的模型都经过 4000 个扩散步骤的训练,在现代 GPU 上生成单个样本需要几分钟的时间,但本文的方法使得我们可以在几秒钟而不是几分钟内从我们的模型中进行采样。
对于使用 T 个扩散步骤训练的模型,我们通常会使用与训练期间使用的相同的
t 值序列 (1, 2, ..., T ) 进行采样。本文使用 t 值的任意子序列
S 进行采样。给定训练噪声表
为了将采样步骤数从 T 减少到 K,使用 1 到 T(含)之间的 K 个均匀间隔的实数,然后将每个结果数字舍入到最接近的整数。
使用此模型,100 个采样步骤足以为完全训练的模型实现接近最佳的 FID
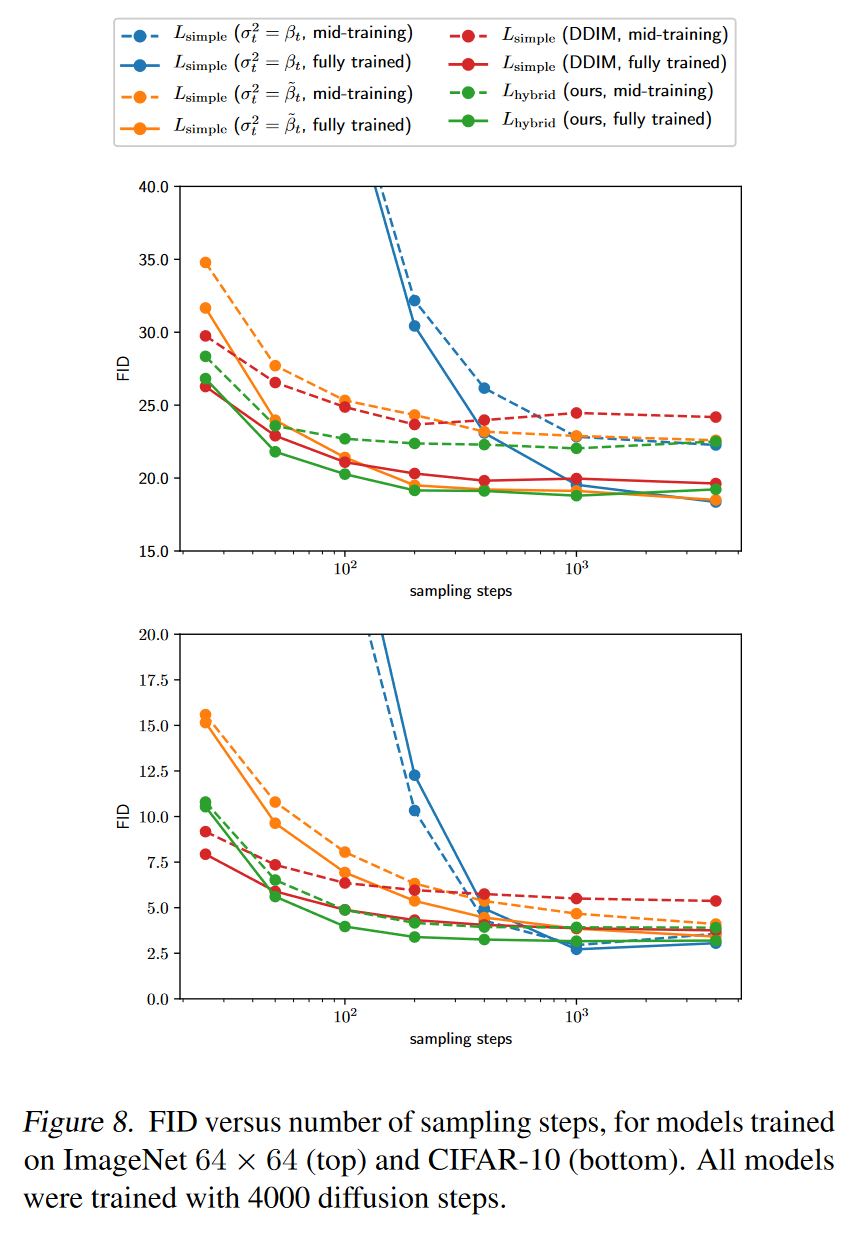
2.3 Scaling Model Size
为了衡量性能如何随着训练计算而扩展,使用 Lhybrid 目标在 ImageNet 64 × 64 上训练四个不同的模型。
- 为了改变模型容量,我们在所有层上应用深度乘数,使得第一层具有 64、96、128 或 192 个通道。(之前的实验在第一层使用了 128 个通道。)
- 由于每层的深度都会影响初始权重的规模,因此我们将每个模型的 Adam
学习率缩放为
,使得 128 通道模型的学习率为 0.0001 (正如其他实验一样)。